子非鱼的技术博客

UDP编程

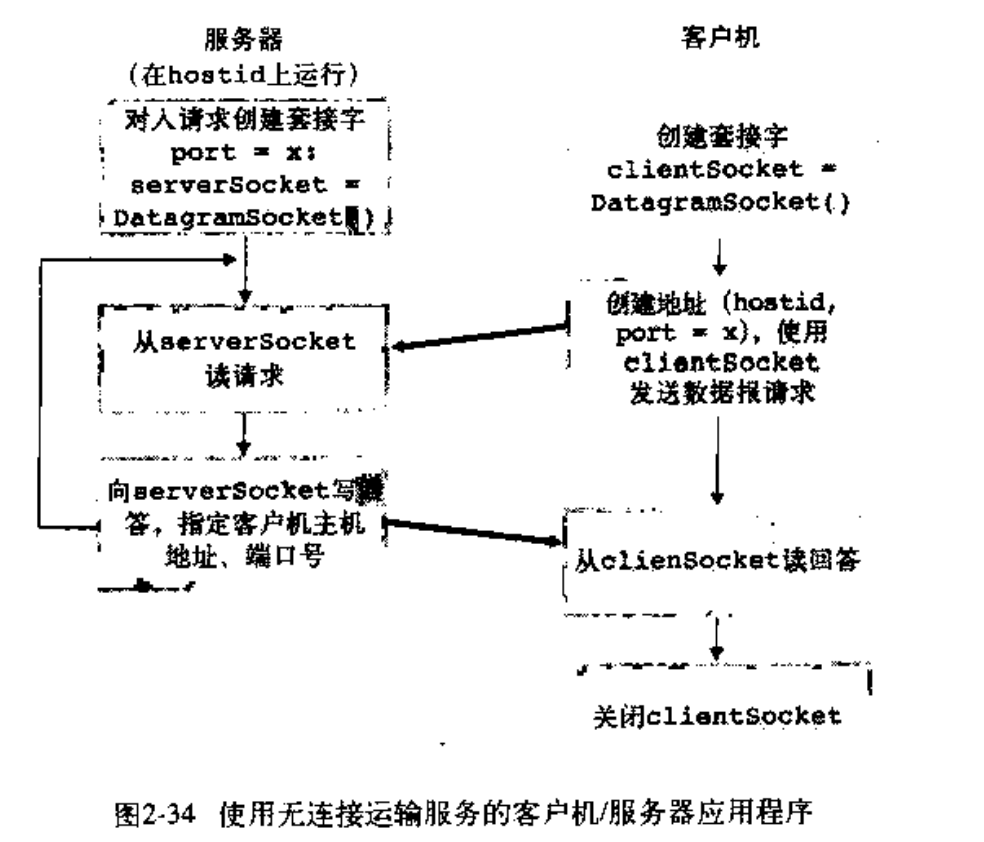
UdpClient

1
2
3
4
5
6
7
8
9

from socket import *
serverName = "hostname"
severPort = 12000
clientSocket = socket(AF_INET,SOCK_DGRAM) # ipv4,udp
message = "Hello World"
clientSocket.sendto(message.encode(),(serverName,severPort))
modifiedMessage,serverAddress = clientSocket.recvfrom(2048)
print(modifiedMessage.decode)
clientSocket.close()

Udpserver

1
2
3
4
5
6
7
8
9

from socket import *
serverPort = 12000
serverSocket = socket(AF_INET, SOCK_DGRAM)  # ipv4,udp
serverSocket.bind(('', serverPort))
print("The server is ready to receive")
while True:
    message, clientAddress = serverSocket.recvfrom(2048)
    modifiedMssage = message.decode().upper()
    serverSocket.sendto(modifiedMssage.encode(), clientAddress)

TCP编程

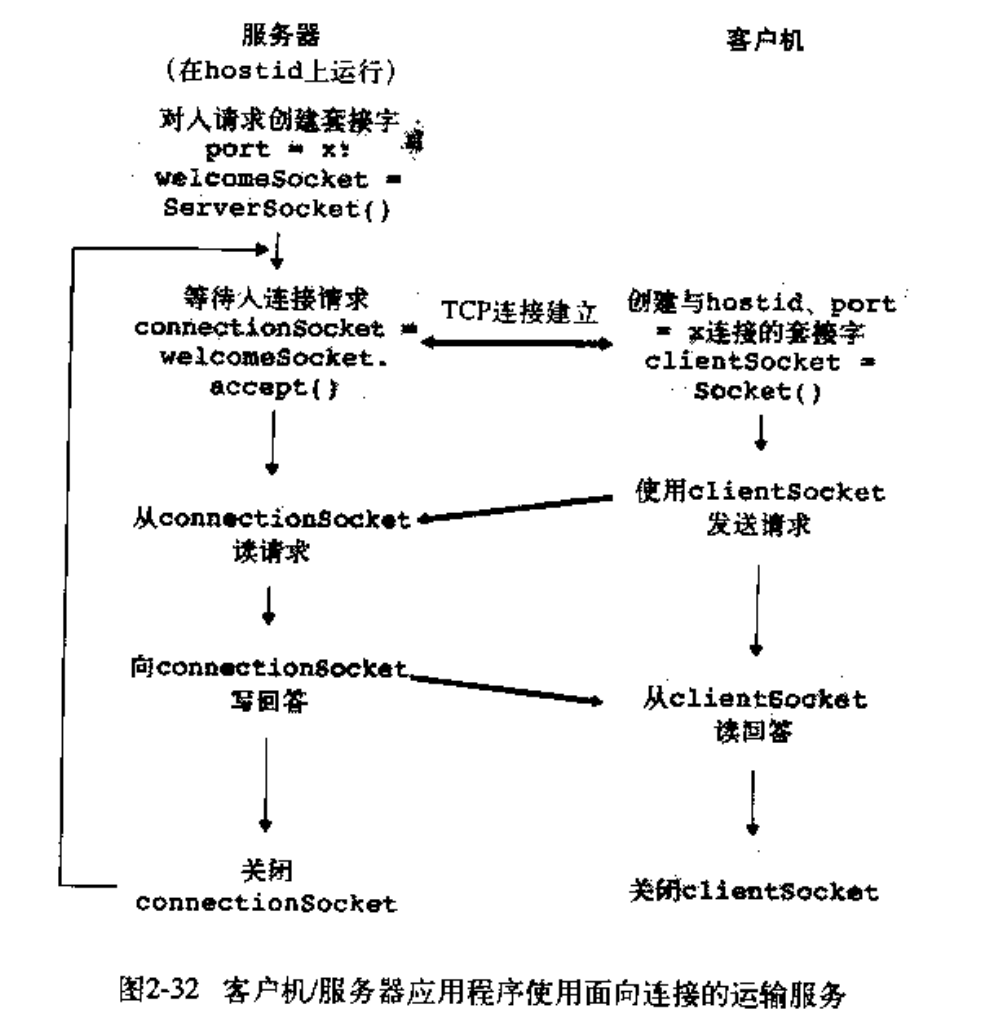
TcpClient

1
2
3
4
5
6
7
8
9

from socket import *
serverName = "servername"
serverPort = 12000
clientSocket = socket(AF_INET,SOCK_STREAM) #ipv4,tcp
clientSocket.connect((serverName,serverPort))
sentence = "Hello World"
clientSocket.send(sentence.encode()) # tcp three-way handshake to welcomesocket
modifiedSentence = clientSocket.recv(1024)
clientSocket.close()

应用层协议原理

传输层向应用层提供的服务为socket API

socket

简化本主机应用层向传输层发送的非有效信息，通过socket代表一组信息

TCP socket包含源IP，源端口，目标IP，目标端口，连接状态

UDP socket包含源IP，源端口

但是传输报文时必须提供对方IP，port。接收报文时传输层需要上传对方的IP，port

Web和HTTP

http为无状态协议，状态通过cookies实现

基础概念

网络：由节点和边组成的结构

计算机网络：由主机节点（主机）和数据交换结点（数据的转发，如路由器交换机）构成的网络，边称为数据链路。

还可分为网络边缘（主机），网络核心（数据交换），接入（连接网络边缘和网络核心）

P2P（peer）：分布式处理，客户端也可以是服务端

吞吐量：在源主机和目标主机之间的有效传输速率

网络核心

电路交换：独享资源，保证性能（计算机之间的通信有突发性，使用该方法则浪费的片较多）

分组交换：不独占资源，数据分组，存储转发（存在排队延迟和丢失，维护队列，超过长度则丢弃分组）

网络资源（如带宽）分成片：时分，频分，波分，码分

传输层：进程到进程

网络层：端到端（end to end），网络设备到网络设备

数据链路层：点到点（point to point）

物理层：数字信号与物理信号的转换

什么问题适合用前缀和

适用于快速、频繁地计算一个索引区间内的元素之和

前缀和算法框架

一维

每次累加前缀，当前元素指的是0-i的前缀和

注：从1开始是为了避免边界另外讨论，sum_list大小为原数组大小+1。填充的边界为0

1
2
3

for (int i = 1; i < sum_list.size(); i++) {
  sum_list[i] = sum_list[i - 1] + sum_list[i - 1];
}

二维

当前元素表示的是0-i，0-j范围内的前缀和

注：从1开始是为了避免边界另外讨论，sum_list长宽为原矩阵大小+1。填充的边界为0

回溯框架

回溯算法求解时要考虑三个问题

1. 路径：已经做出的选择
2. 选择列表：当前可以做的选择，即孩子结点的情况（剪枝做的就是精简孩子结点，避免重复讨论，反映到代码里就是对于某些情况直接continue调过）
3. 结束条件：何时到达决策树的底层，返回结果

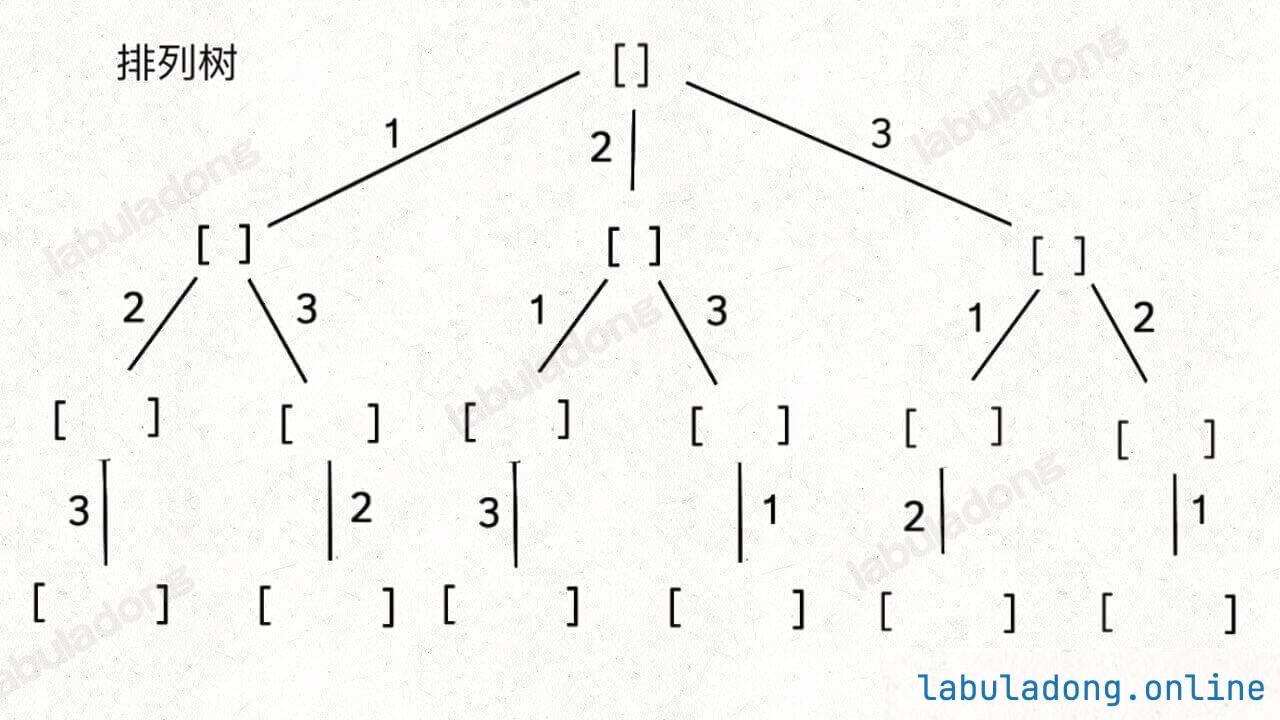
求解的关键在于画出决策树，并运用合理的剪枝条件。不要跳出此框架自己去想新写法，很容易漏解或者多解

1
2
3
4
5
6
7
8
9
10

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

全排列问题

排列问题（元素不重复不可复选）

选择列表：避免选当前路径上已经选择过的数字

解决方法：引入used数组，记录从根结点到当前结点的路径信息，判断数字是否被使用

什么问题适合用动态规划（最优子结构）

符合最优子结构的问题适合用动态规划

最优子结构 是指一个问题的最优解可以通过其子问题的最优解构造出来。换句话说，问题的最优解依赖于子问题的最优解。

例如要计算年级的最高分，可通过计算每个班级的最高分之后取最值得到

动态规划算法框架

确定状态和选择

明确当前值需要通过哪些子结构通过哪些选择得到，用以确定dp数组是一维还是二维的

例如对于斐波那契数列只要知道前2项即可，所以是一维的

对于零钱兑换问题，如果target=10，则粗略估计需要知道0-9的最小值（列），而且要对于不同零钱选择（行）计算最值（也可用一维的做，但二维从语意上更明确）

定义dp数组

什么问题适用滑动窗口

对于连续子序列问题，可以使用滑动窗口。例如按要求得到最长/短的序列

滑动窗口算法框架

1
2
3
4
5
6
7
8
9
10
11
12
13

int low = 0, high = 0;

while (high < nums.size()) {
    // 增大窗口
    window.addLast(nums[high]);
    high++;
    
    while (window needs shrink) {
        // 缩小窗口
        window.removeFirst(nums[low]);
        low++;
    }
}

滑动窗口方法需要考虑两个问题

1. 何时满足题目条件

   可能需要用到哈希表来统计元素出现情况

2. 何时缩小范围

   当high移动到第一次（不）满足题目要求后，移动low来缩小范围

3. 何时记录结果

   如果要记录最长序列则在缩小范围前记录

   如果要记录最短序列则在缩小范围后记录

最小覆盖子串

题目

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

示例 1：

序言

二叉树题型的算法主要分为回溯，动态规划，迭代三类。从本质上三者都是在遍历算法基础上的修改。回溯关心的是在每个结点的访问过程中如何更新结果；动态规划关心的是如何拆解出子问题，不具体分析每个结点的状态，而是通过划分子问题让其通过基本问题递归解决；迭代主要是指BFS层序遍历，适用于与深度（或高度）相关的问题求解

二叉树基本结构

1. 二叉树

1
2
3
4
5
6
7

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

2. 多叉树

1
2
3
4
5

class TreeNode {
public:
    int val;
    vector<TreeNode *> children;
};

二叉树遍历

1. 递归遍历

前序位置：刚进入当前子树根结点的时候（已知根结点信息）

如何写一个递归算法

1. 确定问题：给当前的算法一个符合计算机处理流程的解释。例如对于斐波那契数数列求解int fib(int n)，应该翻译成计算数列第n项并返回数列的值

2. 解决基准问题：思考当输入值为基础值时，其返回的结果是什么。该步用于确定递归终止条件。例如对于汉诺塔问题，在只有一块积木时只需要将其从From移到Target即可

3. 拆解问题：考虑在当前的普通输入时，应该如何解决问题。例如对于斐波那契数数列求解，当前应该返回的值是fib(n-1)+fib(n-2)。

   ❗️❗️不要尝试去思考其内部具体是如何执行的，只要把当前函数当作一个已经实现的库函数即可。否则只会越绕越晕。

递归算法举例分析

二叉树遍历

1. 确定问题：遍历以root为根结点的二叉树
2. 解决基准问题：当root为空指针时返回
3. 拆解问题：在访问完当前结点后，继续遍历左子树（具体说：遍历以root->left为根结点的二叉树），继续遍历右子树（具体说：遍历以root->right为根结点的二叉树）